In probability and statistics, the log-normal distribution is the probability distribution of any random variable whose logarithm is normally distributed. If Y is a random variable with a normal distribution, then X = exp(Y) has a log-normal distribution; likewise, if X is log-normally distributed, then log(X) is normally distributed.
"Log-normal" is also written "log normal" or "lognormal".
A variable might be modeled as log-normal if it can be thought of as the multiplicative product of many small independent factors. For example the long-term return rate on a stock investment can be considered to be the product of the daily return rates.

Characterization
The log-normal distribution has the probability density function

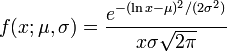
for x > 0, where μ and σ are the mean and standard deviation of the variable's logarithm (by definition, the variable's logarithm is normally distributed).

Probability density function

Cumulative distribution function


Properties
The expected value is

and the variance is

Equivalent relationships may be written to obtain μ and σ given the expected value and standard deviation:



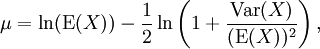
Mean and standard deviation
The geometric mean of the log-normal distribution is exp(μ), and the geometric standard deviation is equal to exp(σ).
If a sample of data is determined to come from a log-normally distributed population, the geometric mean and the geometric standard deviation may be used to estimate confidence intervals akin to the way the arithmetic mean and standard deviation are used to estimate confidence intervals for a normally distributed sample of data.
Where geometric mean μ_geo = exp(μ) and geometric standard deviation σ_geo = exp(σ)

Geometric mean and geometric standard deviation
The first few raw moments are:





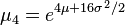
Moments
The partial expectation of a random variable X with respect to a threshold k is defined as

where f(x) is the density. For a lognormal density it can be shown that

where Φ is the cumulative distribution function of the standard normal. The partial expectation of a lognormal has applications in insurance and in economics (for example it can be used to derive the Black-Scholes formula).

Partial expectation
For determining the maximum likelihood estimators of the log-normal distribution parameters μ and σ, we can use the same procedure as for the normal distribution. To avoid repetition, we observe that

where by we denote the density probability function of the log-normal distribution and by —that of the normal distribution. Therefore, using the same indices to denote distributions, we can write the log-likelihood function thus:

Since the first term is constant with regards to μ and σ, both logarithmic likelihood functions, and , reach their maximum with the same μ and σ. Hence, using the formulas for the normal distribution maximum likelihood parameter estimators and the equality above, we deduce that for the log-normal distribution it holds that


Related distributions

Robert Brooks, Jon Corson, and J. Donal Wales. "The Pricing of Index Options When the Underlying Assets All Follow a Lognormal Diffusion", in Advances in Futures and Options Research, volume 7, 1994.